Use of machine learning in multi-scale finite element simulations
Use of machine learning in multi-scale finite element simulations
Almost all materials have a heterogeneous microstructure, which, however, in in numerical simulations of the mechanical or mechanical or thermal-mechanical material behavior is generally not explicitly taken into account. Instead, the material behavior is modeled using phenomenological material models, which are created for the respective material and material and calibrated with experimental data. In order to take the heterogeneous microstructure into account, for fibre-reinforced polymers, for example, multi-scale finite element element simulations (so-called FE² simulations) can be used. Here, the macroscopic component behavior is simulated by using the phenomenological material model, a microstructure in the form of a representative a microstructure in the form of a representative volume element is calculated.
Performing multi-scale finite element simulations is very time-consuming and resource-intensive in terms of computing power, especially for complex material behavior. As a result, questions of uncertainty quantification and optimization in relation to the microstructure are not feasible. The main reason for the high costs lies in the large number of evaluations of the microstructure, which from a mathematical point of view requires the solution of an initial boundary value problem in each case. Therefore, the development of substitute models for the evaluation of the microstructure is of particular interest. As part of the cooperation between the Institute of Engineering Mechanics and the Institute for Software and Systems Engineering, machine learning methods are used to create substitute models for microstructure evaluation. These substitute models are then used in multi-scale finite element simulations. Neural networks are of particular interest for the development of the surrogate models, as they can be evaluated very quickly after prior training and thus accelerate the evaluation of the microstructure enormously. Initially, data-based approaches are pursued and, building on this, an extension to physically-informed surrogate models is developed in order to ensure consistency with the underlying physical equations. Another focus is not to replace the microstructure with a surrogate model - in contrast to the usual approach in the literature - but to accelerate the calculation of the microstructure itself using surrogate models. This step facilitates the consideration of complex material behaviour in the microstructure and enables the implementation of uncertainty quantification and optimization at the microstructure level.
Research results
Data-based deep neural networks as a replacement model
A neural network was created as a data-based substitute model for a microstructure that includes linear and non-linear elastic material behavior. Different network architectures were examined and compared. By using derivative information (so-called Sobolev training), the amount of required training data was significantly reduced and the accuracy of the surrogate model was increased. The use of just-in-time compilation and an efficient implementation of the trained neural network in the finite element program at the Institute of Engineering Mechanics resulted in a calculation that was up to 6000 times faster than a reference simulation. The neural network thus replaces an iterative procedure for calculating the mechanical microstructure response for a given load with a simple function evaluation. This makes it possible to perform multi-scale finite element simulations with low computational effort and high accuracy of the results.
Deep operator networks for physically-informed surrogate models
Instead of replacing microstructure evaluation with a data-based neural network, deep operator networks enable the detailed calculation of mechanical variables at microstructure level, taking into account the basic physical equations. To this end, deep operator networks are being further developed by coupling them with model reduction approaches (proper orthogonal decomposition). This significantly reduces the amount of training data required and allows the use of known material models from mechanics. For the first time, hybrid solvers consisting of finite elements for the macroscale and deep operator networks for the microscale were used. The calculation could be carried out up to 300 times faster with simultaneous calculation of all essential variables of the microstructure.
Publication list
- H. Eivazi, M. Alikhani, J.-A. Tröger, S. Wittek, S. Hartmann, A. Rausch. Enhancing multiscale simulations with constitutive relations-aware deep operator networks. arXiv preprint arXiv:2405.13759 [cs.LG], 2024, DOI: 10.48550/arxiv.2405.13759
- J.-A. Tröger, H. Eivazi, S. Hartmann, S. Wittek, A. Rausch. Efficient integration of deep neural networks in sequential multiscale simulations. Proceedings in Applied Mechanics and Mathematics, 23(4), e202300052, 2023, DOI: 10.1002/pamm.202300052
- H. Eivazi, J.-A. Tröger, S. Wittek, S. Hartmann, A. Rausch. FE² computations with deep neural networks: Algorithmic structure, data generation and implementation. Mathematical and Computational Applications, 28(4), 2023. DOI: 10.3390/mca28040091
Contact
- Research group Solid Mechanics: Prof. Stefan Hartmann, M.Sc. Jendrik-Alexander Tröger
- Research group Machine Learned Models for Engineers: Prof. Andreas Rausch, Dr. Stefan Wittek, M.Sc. Hamidreza Eivazi
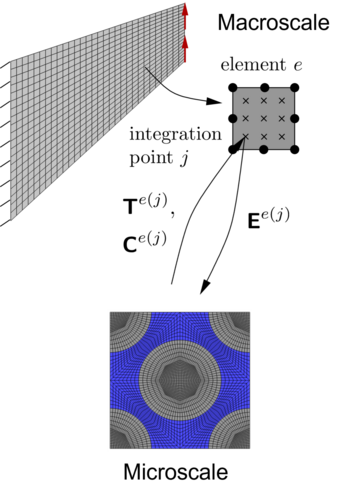
Schematic illustration of multi-scale finite element simulations including a microstructure
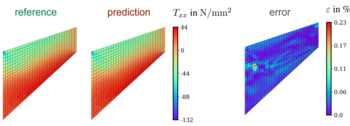
Illustration of the reference solution (left), prediction of the data-based neural network (center) and relative error (right)
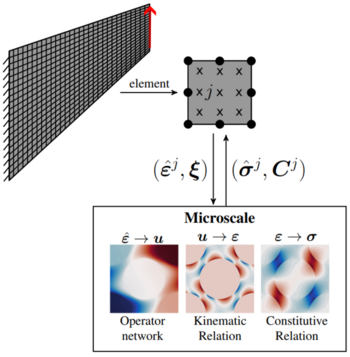
Schematic illustration of the procedure for using physically-informed deep operator networks (DeepONets) for the microstructure