Einsatz von maschinellem Lernen in mehrskaligen Finite Elemente Simulationen
Einsatz von maschinellem Lernen in mehrskaligen Finite Elemente Simulationen
Nahezu alle Materialien verfügen über eine heterogene Mikrostruktur, welche allerdings in numerischen Simulationen des mechanischen oder auch thermisch-mechanischen Materialverhaltens in der Regel nicht explizit berücksichtigt wird. Stattdessen wird das Materialverhalten über sogenannte phänomenologische Materialmodelle modelliert, welche für das jeweilige Material erstellt und mit experimentellen Daten kalibriert werden. Um die heterogene Mikrostruktur zu berücksichtigen, beispielsweise für faserverstärkte Polymere, können mehrskalige Finite Elemente Simulationen (sogenannte FE²-Simulationen) herangezogen werden. Dabei wird das makroskopische Bauteilverhalten simuliert, indem statt des phänomenologischen Materialmodells eine Mikrostruktur in Form eines repräsentativen Volumenelementes berechnet wird.
Die Durchführung mehrskaliger Finite Elemente Simulationen ist insbesondere für komplexes Materialverhalten sehr zeit- und im Hinblick auf die Rechenleistung ressourcenintensiv. Dadurch sind Fragestellungen der Unsicherheitsquantifizierung und Optimierung in Bezug auf die Mikrostruktur nicht durchführbar. Die wesentliche Ursache der hohen Kosten liegt in der Vielzahl von Auswertungen der Mikrostruktur, was aus mathematischer Sicht jeweils die Lösung eines Anfangs-Randwertproblems erfordert. Daher ist die Entwicklung von Ersatzmodellen für die Auswertung der Mikrostruktur von besonderem Interesse. Im Rahmen der Kooperation zwischen dem Institut für Technische Mechanik und dem Institute for Software and Systems Engineering werden Methoden des maschinellen Lernens genutzt, um Ersatzmodelle für die Mikrostrukturauswertung zu erstellen. Diese Ersatzmodelle werden anschließend in mehrskaligen Finite Elemente-Simulationen genutzt. Für die Entwicklung der Ersatzmodelle sind insbesondere neuronale Netze von Interesse, da diese nach vorherigem Training sehr schnell auswertbar sind und damit die Auswertung der Mikrostruktur enorm beschleunigen. Zunächst werden datenbasierte Ansätze verfolgt und darauf aufbauend eine Erweiterung auf physikalisch-informierte Ersatzmodelle entwickelt, um die Konsistenz zu den zugrundeliegenden physikalischen Gleichungen zu gewährleisten. Ein weiterer Schwerpunkt liegt darin die Mikrostruktur – im Gegensatz zur üblichen Vorgehensweise in der Literatur – nicht durch ein Ersatzmodell zu ersetzen, sondern die Berechnung der Mikrostruktur an sich durch Ersatzmodelle zu beschleunigen. Dieser Schritt erleichtert die Berücksichtigung von komplexem Materialverhalten in der Mikrostruktur und ermöglicht die Durchführung von Unsicherheitsquantifizierung und Optimierung auf Mikrostruktur-Ebene.
Forschungsergebnisse
Datenbasierte tiefe neuronale Netze als Ersatzmodell
Für eine Mikrostruktur, die linear und nicht-linear elastisches Materialverhalten umfasst, wurde ein neuronales Netz als datenbasiertes Ersatzmodell erstellt. Dabei wurden unterschiedliche Netz-Architekturen untersucht und verglichen. Durch Nutzung von Ableitungsinformationen (sogenanntes Sobolev-Training) wurde der Umfang an benötigten Trainingsdaten wesentlich reduziert und die Genauigkeit des Ersatzmodells gesteigert. Die Verwendung von just-in-time compilation und eine effiziente Implementierung des trainierten neuronalen Netzes in das Finite Elemente-Programm am Institut für Technische Mechanik resultierte in einer bis zu 6000 Mal schnelleren Berechnung im Vergleich zu einer Referenzsimulation. Das neuronale Netz ersetzt damit ein iteratives Verfahren zur Berechnung der mechanischen Mikrostruktur-Antwort für eine gegebene Belastung durch eine einfache Funktionsauswertung. Damit ist es möglich mehrskalige Finite Elemente Simulationen mit geringem Rechenaufwand bei gleichzeitig hoher Genauigkeit der Ergebnisse durchzuführen.
Tiefe Operatornetzwerke für physikalisch-informierte Ersatzmodelle
Anstatt die Mikrostruktur-Auswertung durch ein datenbasiertes neuronales Netz zu ersetzen, ermöglichen tiefe Operatornetzwerke (deep operator networks) die detaillierte Berechnung mechanischer Größen auf Mikrostruktur-Ebene unter Einbeziehung der physikalischen Grundgleichungen. Dafür erfolgt eine Weiterentwicklung der tiefen Operatornetzwerke durch Kopplung mit Modellreduktionsansätzen (proper orthogonal decomposition). Dadurch wird der Umfang an erforderlichen Trainingsdaten wesentlich reduziert und die Nutzung bekannter Materialmodelle aus der Mechanik kann erfolgen. Zum ersten Mal wurden damit hybride Solver aus Finiten Elementen für die Makroskala und tiefen Operatornetzwerken für die Mikroskala verwendet. Die Berechnung konnte bei gleichzeitiger Berechnung aller wesentlichen Größen der Mikrostruktur bis zu 300 Mal schneller erfolgen.
Veröffentlichungen
- H. Eivazi, M. Alikhani, J.-A. Tröger, S. Wittek, S. Hartmann, A. Rausch. Enhancing multiscale simulations with constitutive relations-aware deep operator networks. arXiv preprint arXiv:2405.13759 [cs.LG], 2024, DOI: 10.48550/arxiv.2405.13759
- J.-A. Tröger, H. Eivazi, S. Hartmann, S. Wittek, A. Rausch. Efficient integration of deep neural networks in sequential multiscale simulations. Proceedings in Applied Mechanics and Mathematics, 23(4), e202300052, 2023, DOI: 10.1002/pamm.202300052
- H. Eivazi, J.-A. Tröger, S. Wittek, S. Hartmann, A. Rausch. FE² computations with deep neural networks: Algorithmic structure, data generation and implementation. Mathematical and Computational Applications, 28(4), 2023. DOI: 10.3390/mca28040091
Berichterstattung über das Projekt
Kontakt
- AG Festkörpermechanik: Prof. Stefan Hartmann, M.Sc. Jendrik-Alexander Tröger
- AG Machine Learned Models for Engineers: Prof. Andreas Rausch, Dr. Stefan Wittek, M.Sc. Hamidreza Eivazi
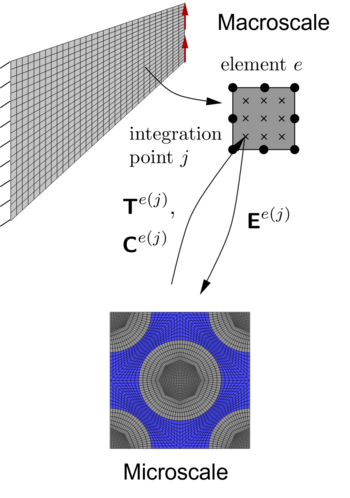
Schematische Darstellung von mehrskaligen Finite Element Simulationen unter Einbeziehung einer Mikrostruktur
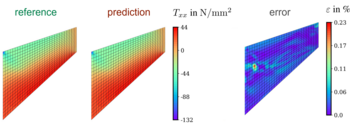
Darstellung der Referenzlösung (links), Vorhersage des datenbasierten neuronalen Netzes (mitte) und relativer Fehler (rechts)
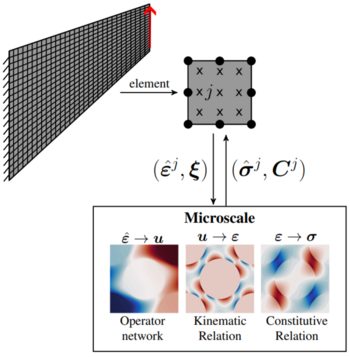
Schematische Darstellung der Vorgehensweise bei Nutzung physikalisch-informierter tiefer Operatornetze (DeepONets) für die Mikrostruktur